Question

In a study of academic procrastination, the authors of a paper reported that for a sample of 471 undergraduate students at a midsize public university preparing for a final exam in an introductory psychology course, the mean time spent studying for the exam was 7.14 hours and the standard deviation of study times was 3.20 hours. For purposes of this exercise, assume that it is reasonable to regard this sample as representative of students taking introductory psychology at this university.

Construct a 95% confidence interval to estimate μ, the mean time spent studying for the final exam for students taking introductory psychology at this university.

Answer 1

95% confidence interval for the mean time spent studying for the final exam for students taking introductory psychology at this university is [6.85 hours, 7.43 hours].

Explanation:

We are given that a sample of 471 undergraduate students at a midsize public university preparing for a final exam in an introductory psychology course, the mean time spent studying for the exam was 7.14 hours and the standard deviation of study times was 3.20 hours.

Firstly, the pivotal quantity for 95% confidence interval for the population mean is given by;

P.Q. =
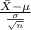`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean time spent studying for the exam = 7.14 hours

`\sigma` = population standard deviation = 3.20 minutes

n = sample of undergraduate students = 471

`\mu` = population mean time

Here for constructing 95% confidence interval we have used One-sample z test statistics.

So, 95% confidence interval for the population mean,
`\mu` is ;

P(-1.96 < N(0,1) < 1.96) = 0.95 {As the critical value of z at 2.5% level

of significance are -1.96 & 1.96}

P(-1.96 <
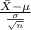`(\bar X-\mu)/((\sigma)/(√(n) ) )` < 1.96) = 0.95

P(
`-1.96 * {(\sigma)/(√(n) ) }` <
`{\bar X-\mu}` <
`1.96 * {(\sigma)/(√(n) ) }` ) = 0.95

P(
`\bar X-1.96 * {(\sigma)/(√(n) ) }` <
`\mu` <
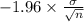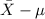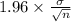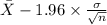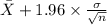`\bar X+1.96 * {(\sigma)/(√(n) ) }` ) = 0.95

95% confidence interval for
`\mu` = [
`\bar X-1.96 * {(\sigma)/(√(n) ) }` ,
`\bar X+1.96 * {(\sigma)/(√(n) ) }` ]

= [
`7.14-1.96 * {(3.20)/(√(471) ) }` ,
`7.14+1.96 * {(3.20)/(√(471) ) }` ]

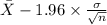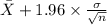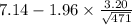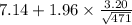= [6.85 hours , 7.43 hours]

Therefore, 95% confidence interval for the mean time spent studying for the final exam for students taking introductory psychology at this university is [6.85 hours, 7.43 hours].