Question

X/x-1 - (-2)/x+1 subtract and simplify

Answer 1

Answer:
`(x^2+3x-2)/((x-1)(x+1))`

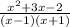
Explanation:

`(x)/(x-1) - (-2)/(x+1)`

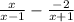
To simplify this, we must first set the fractions' denominators to match.

We can do this by multiplying each fraction by the other's denominator, as follows:

`(x(x+1))/((x-1)(x+1)) - (-2(x-1))/((x-1)(x+1))`

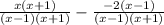
Then, you can subtract them, keeping the denominators the same:

`(x(x+1)+2(x-1))/((x-1)(x+1))`

Them, simplify the equation:

`(x^2+3x-2)/((x-1)(x+1))`

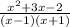
This is the most simplified form of this expression, as the quadratic expression in the numerator cannot be factored.