Question

What is the value of tan?

Answer 1

Answer: B.
`(4)/(3)` .

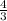Explanation:

• In a right triangle, the ratios of its sides are called trigonometric ratios.
• The three common trigonometric ratios are the sine (sin), cosine (cos), and tangent (tan).

We have given ,
`\sin\theta=(4)/(5)\text{ and }(\pi)/(2)<\theta<(3\pi)/(2)`.

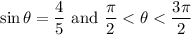Then,
`\cos\theta =√(1-\sin^2\theta)\ [\because\ \sin^2A+\cos^2A=1]`

Put value of
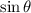`\sin\theta`, we get

`\Rightarrow\ \cos\theta=\sqrt{1-((4)/(5))^2}`

`\Rightarrow=\sqrt{1-(16)/(25)}=\sqrt{(25-16)/(25)}=\sqrt{(9)/(25)}=(3)/(5)`

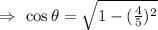
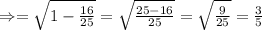
Now , as we know ,
`\tan\theta=(\sin\theta)/(\cos\theta)=((4)/(5))/((3)/(5))=(4)/(3)`

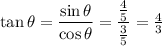
Hence, the correct option is B.
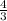`(4)/(3)` .