Question

1. Let a be a positive real number. In Part (1) of Theorem 3.25, we proved that for each real number x, jxj < a if and only if a < x < a. It is important to realize that the sentence a < x < a is actually the conjunction of two inequalities. That is, a < x < a means that a < x and x < a. ? (a) Complete the following statement: For each real number x, jxj a if and only if . . . . (b) Prove that for each real number x, jxj a if and only if a x a. (c) Complete the following statement: For each real number x, jxj > a if and only if .

Answer 1

(a)

if
`x \geq 0` then
`x \geq a` and if x<0 then
`-x > a`

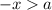
(b)

That is straightforward from what you showed on theorem 3.25

(c)

Following the same ideas from (a) x>a or -x > a.

Explanation:

Remember how we define the absolute value of a number.

(a)

In general

`|x| = x \,\,\,\text{if} \,\,\,\, x \geq 0 \\|x| = -x \,\,\,\text{if} \,\,\,\, x < 0`

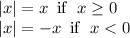
Therefore if
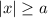`|x| \geq a` you have two cases, if
`x \geq 0` then
`x \geq a` and if x<0 then
`-x > a`

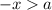
(b)

That is straightforward from what you showed on theorem 3.25

(c)

Following the same ideas from (a) x>a or -x > a.