Question

Tensile-strength tests were carried out on two different grades of wire rod. Grade 1 has 10 observations yielding a sample mean of 1085 and a standard deviation of 52. Grade 2 has 15 observations yielding a sample mean of 1034 and a standard deviation of 61. Assume the populations to be approximately normal with equal variances. State and conclude your hypothesis at the 0.05 level of significance if grade 1 and grade 2 true means are equal to each other.

Answer 1

`t=\frac{(1085 -1034)-(0)}{57.646\sqrt{(1)/(10)+(1)/(15)}}=2.167`

`p_v =2*P(t_(23)<-2.167) =0.0408`

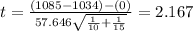
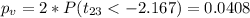
We see that the p value is lower than the significance level provided of 0.05 so then we have enough evidence to conclude that the true means are different at 5% of significance.

Explanation:

Data given

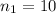`n_1 =10` represent the sample size for group 1

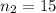`n_2 =15` represent the sample size for group 2

`\bar X_1 =1085` represent the sample mean for the group 1

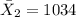`\bar X_2 =1034` represent the sample mean for the group 2

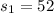`s_1=52` represent the sample standard deviation for group 1

`s_2=61` represent the sample standard deviation for group 2

We are assuming that the two samples are normally distributed with equal variances and that means:

`\sigma^2_1 =\sigma^2_2 =\sigma^2`

System of hypothesis

Null hypothesis:
`\mu_1 = \mu_2`

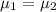
Alternative hypothesis:
`\mu_1 \\eq \mu_2`

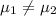
The statistic is given by:

`t=\frac{(\bar X_1 -\bar X_2)-(\mu_(1)-\mu_2)}{S_p\sqrt{(1)/(n_1)+(1)/(n_2)}}`

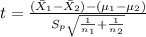
The degrees of freedom are given by:

`n_1+n_2 -2`

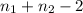
And the pooled variance is:

`S^2_p =((n_1-1)S^2_1 +(n_2 -1)S^2_2)/(n_1 +n_2 -2)`

Replacing we got:

`S^2_p =((10-1)(52)^2 +(15 -1)(61)^2)/(10 +15 -2)=3323.043`

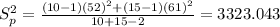
And the deviation would be:

`S_p=57.646`

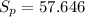
The degrees of freedom are:

`df=10+15-2=23`

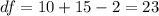
The statistic would be:

`t=\frac{(1085 -1034)-(0)}{57.646\sqrt{(1)/(10)+(1)/(15)}}=2.167`

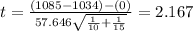
The p value would be

`p_v =2*P(t_(23)<-2.167) =0.0408`

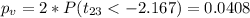
We see that the p value is lower than the significance level provided of 0.05 so then we have enough evidence to conclude that the true means are different at 5% of significance.