Question

In ΔPQR, the measure of ∠R=90°, RQ = 80, PR = 39, and QP = 89. What is the value of the tangent of ∠Q to the nearest hundredth?

Answer 1

56

Explanation:

In ΔPQR, the measure of ∠R=90°, RQ = 80, PR = 39, and QP = 89. What is the value of the tangent of ∠Q to the nearest hundredth?

Answer 2

We have been given that in ΔPQR, the measure of ∠R=90°, RQ = 80, PR = 39, and QP = 89. We are asked to find the value of the tangent of ∠Q to the nearest hundredth.

First of all, we will draw a right triangle with our given information.

We know that tangent relates opposite side of right triangle with its adjacent side.

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

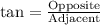
We can see from our diagram that opposite side to angle Q is 39 and adjacent side to angle Q is 80.

`\text{tan}(Q)=(39)/(80)`

`\text{tan}(Q)=0.4875`

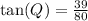
Upon rounding to nearest hundredth, we will get:

`\text{tan}(Q)\approx 0.49`

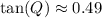
Therefore, the value of tangent of Q is approximately 0.49 units.