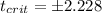Answer:
a)
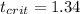
b)
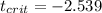
c)
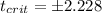
Explanation:
Part a
The significance level given is
 and the degrees of freedom are given by:
and the degrees of freedom are given by:

Since we are conducting a right tailed test we need to find a critical value on the t distirbution who accumulates 0.1 of the area in the right and we got:
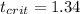
Part b
The significance level given is
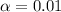 and the degrees of freedom are given by:
and the degrees of freedom are given by:
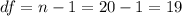
Since we are conducting a left tailed test we need to find a critical value on the t distirbution who accumulates 0.01 of the area in the left and we got:
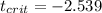
Part c
The significance level given is
 and
and
 and the degrees of freedom are given by:
and the degrees of freedom are given by:
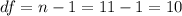
Since we are conducting a two tailed test we need to find a critical value on the t distirbution who accumulates 0.025 of the area on each tail and we got: