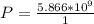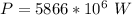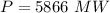Complete Question
A large power plant heats 1917 kg of water per second to high-temperature steam to run its electrical generators.
(a) How much heat transfer is needed each second to raise the water temperature from 35.0°C to 100°C, boil it, and then raise the resulting steam from 100°C to 450°C? Specific heat of water is 4184 J/(kg · °C), the latent heat of vaporization of water is 2256 kJ/kg, and the specific heat of steam is 1520 J/(kg · °C).
J
(b) How much power is needed in megawatts? (Note: In real power plants, this process occurs under high pressure, which alters the boiling point. The results of this problem are only approximate.)
MW
Answer:
The heat transferred is
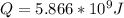
The power is
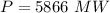
Step-by-step explanation:
From the question we are told that
Mass of the water per second is
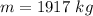
The initial temperature of the water is
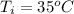
The boiling point of water is
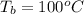
The final temperature
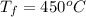
The latent heat of vapourization of water is
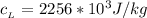
The specific heat of water
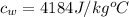
The specific heat of stem is
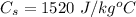
Generally the heat needed each second is mathematically represented as
![Q = m[c_w (T_i - T_b) + m* c__(L)} + m* c__(S)} (T_f - T_b)]](https://img.qammunity.org/2021/formulas/physics/college/qwqx5w6yml8hx7j30ptxxj2hcqbuembvmx.png)
Then substituting the value
![Q = m[c_w [T_i - T_b] + c__(L)} + C__(S)} [T_f - T_b]]](https://img.qammunity.org/2021/formulas/physics/college/zbp3c7rm7kmgbaszs9gukahdc72wzff76r.png)
![Q = 1917 [(4184) [100 - 35] + [2256 * 10^3] +[1520] [450 - 100]]](https://img.qammunity.org/2021/formulas/physics/college/lpo0wf2v8pztul3bawqz7hxwwwwqd4a3k4.png)
![Q = 1917 * [3.05996 * 10^6]](https://img.qammunity.org/2021/formulas/physics/college/jijkrzex2og91eh7j8gq5tmeyvw7jddb7d.png)
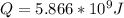
The power required is mathematically represented as
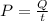
From the question
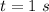
So