Answer:
Check the explanation
Explanation:
Going by the first attached image below we reject H_o against H_1 if obs.
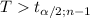
here obs.T=1.879
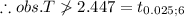
we accept
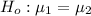 at 5% level of significance.
at 5% level of significance.
i.e there is no sufficient evidence to indicate that the special study program is more effective at 5% level of significance.
1.
this problem is simillar to the previous one except the alternative hypothesis.
Let X_i's denote the bonuses given by female managers and Y_i's denote the bonuses given by male managers.
we assume that
 independently
independently
We want to test

define
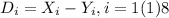
now

the hypothesis becomes
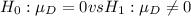
in the third attached image, we use the same test statistic as before
i.e at 5% level of significance there is not enough evidence to indicate a difference in average bonuses .