Answer:
C. 99%
Explanation:
The width of a confidence interval is defined by its margin of error. The smaller the margin of error, the narrower the confidence interval.
This margin of error is proportional to the critical value of z, the standard deviation and inversely proportional to the square root of the sample size.
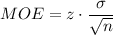
The confidence level affects the critical value z. Increasing the confidence level increase the z-value. Then, it also increases the margin of error and the width of the confidence interval. The higher the confidence level, the widest the confidence interval.
This is logical because we want to increase the confidence about the true mean with the same information (the sample), so the width of the confidence interval has to increase to include more values.