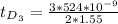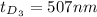Answer:
For constructive interference
The first three thicknesses are
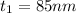
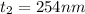
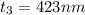
For destructive interference
The first three thicknesses are

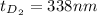
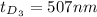
Step-by-step explanation:
The diagram for this question is shown on the first uploaded image
From the question we are told that
The refractive index of oil is
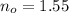
The refractive index of water is
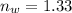
The average wavelength is

For constructive interference the thickness is mathematically represented as
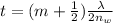
Where m is the order of the interference with a value from
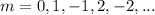
For m = 0
The thickness of the oil slick would be
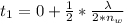
Substituting value
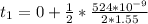
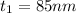
For m = 1
The thickness of the oil slick would be
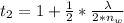
Substituting value
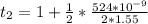
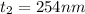
For m = 2
The thickness of the oil slick would be
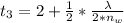
Substituting value
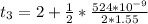
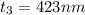
For destructive interference the thickness is mathematically represented as

For m = 1

Substituting value
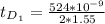

For m = 2
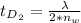
Substituting value
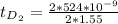
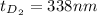
For m = 3

Substituting value