Question

Compare the catching of two different water balloons.

Case A: A 150-ml water balloon moving at 8 m/s is caught and brought to a stop.
Case B: A 600-ml water balloon moving at 8 m/s is caught with the same
technique and brought to a stop.
The collision time is the same for each case.
Case A
Case B
Before
After
Before
After
Which variable is different for these two cases?
Maths
Which Case involves the greatest momentum change?
Which Case involves the greatest impulse?
Which Case involves the greatest force?

Answer 1

In the given scenarios, Case A and Case B involve catching water balloons with different volumes and sizes at the same speed and bringing them to a stop. The volume of the water balloons is the variable that is different between the two cases. Case B involves the greatest momentum change, impulse, and force due to the higher mass of the water balloon.

Step-by-step explanation:

In the given scenario, we have two cases: Case A and Case B, where water balloons of different sizes and volumes are caught and brought to a stop with the same technique at the same speed.

• The variable that is different for these two cases is the volume of the water balloons. In Case A, the water balloon has a volume of 150 ml, while in Case B, the water balloon has a volume of 600 ml.

• When comparing the momentum change, Case B involves the greatest momentum change because momentum is directly proportional to mass. Since the mass of the water balloon in Case B is greater than the mass in Case A, the momentum change in Case B will be greater.

• Similarly, Case B also involves the greatest impulse because impulse is equal to the change in momentum. Since the momentum change is greater in Case B due to the higher mass, the impulse will also be greater.

• Lastly, Case B involves the greatest force because force is equal to the rate of change of momentum. Again, since the momentum change is greater in Case B due to the higher mass, the force will also be greater.

Answer 2

a. The volume V₁ and V₂

b. The case that involves the greatest momentum change = Case B

c. The case that involves the greatest impulse = Case B

d. b. The case that involves the greatest force = Case B

Step-by-step explanation:

Here we have

Case A: V₁ = 150-mL, v₁ = 8 m/s

Case B: V₂ = 600-mL, v₁ = 8 m/s

a. The variable that is different for the two cases is the volume V₁ and V₂

b. The momentum change is by the following relation;

ΔM₁ = Mass, m × Δv₁

The mass of the balloon are;

Δv₁ = Change in velocity = Final velocity - Initial velocity

Mass = Density × Volume

Density of water = 0.997 g/mL

Case A, mass = 150 × 0.997 = 149.55 g

Case B, mass = 600 × 0.997 = 598.2 g

The momentum change is;

Case A: Mass, m × Δv₁ = 149.55 g/1000 × 8 m/s = 1.1964 g·m/s

Case B: Mass, m × Δv₁ = 598.2/1000 × 8 = 4.7856 g·m/s

Therefore Case B has the greatest momentum change

The case that has the gretest momentum change = Case B

c. The momentum change = impulse therefore Case B involves the greatest impulse

d. Here we have;

Impulse = Momentum change =
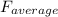`F_(average)` × Δt = mΔV

∴
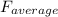`F_(average)` = m·ΔV/Δt

∴ For Case A
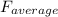`F_(average)` = 149.55×8/Δt = 1196.4/Δt N

For Case B
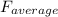`F_(average)` = 598.2×8/Δt = 4785.6/Δt

Where Δt is the same for Case A and Case B,
`F_(average)` for Case B >>
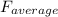`F_(average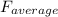)` for Case B

Therefore, Case B involves the greatest force.