Question

What is the value of x?

(1/3)^x-2 =(1/3)^2

Answer 1

Explanation:

Hi there,

To solve this, we want to isolate x either using logs or exponent rules. For this, I chose exponent rules.

First, divide both sides of the equation by (1/3)² :

`((((1)/(3) )^(x-2) ))/(((1)/(3) )^(2) ) = (((1)/(3) )^(2) )/(((1)/(3) )^(2) ) \\`

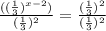
The right-hand side is reduced to 1. The left-hand side contains values that have the same base, so we can use this exponent rule:

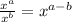`(x^(a) )/(x^(b) ) =x^(a-b)` Apply this:

`((1)/(3))^(x-2-2)=((1)/(3))^(x-4)=1` Now, we are left with:

`((1)/(3))^(x-4)=1`

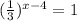
Conceptually, you just have to think: what exponent can make a base equal to 1?

This is based on the following exponent rule:

`x^(0) =1`

So, all we have to do is set (x-4) = 0!

`x-4=0\\x=4`

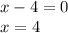
Thus, the value of x is 4.

If you liked this solution, hit Thanks or give a Rating!