Question

15. Suppose a box of 30 light bulbs contains 4 defective ones. If 5 bulbs are to be removed out of the box.

1) What is the probability that all 5 are good?






2) What is the probability that at most two bulbs are defective?






3) What is the probability that at least one bulb is defective?

Answer 1

1) Probability that all five are good = 0.46

2) P(at most 2 defective) = 0.99

3) Pr(at least 1 defective) = 0.54

Explanation:

The total number of bulbs = 30

Number of defective bulbs = 4

Number of good bulbs = 30 - 4 = 26

Number of ways of selecting 5 bulbs from 30 bulbs =
`30C5 = (30 !)/((30-5)!5!) \\`

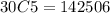`30C5 = 142506` ways

Number of ways of selecting 5 good bulbs from 26 bulbs =
`26C5 = (26 !)/((26-5)!5!) \\`

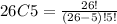
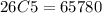`26C5 = 65780` ways

Probability that all five are good = 65780/142506

Probability that all five are good = 0.46

2) probability that at most two bulbs are defective = Pr(no defective) + Pr(1 defective) + Pr(2 defective)

Pr(no defective) has been calculated above = 0.46

Pr(1 defective) =
`(26C4 * 4C1)/(30C5)`

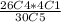
Pr(1 defective) = (14950*4)/142506

Pr(1 defective) =0.42

Pr(2 defective) =
`(26C3 * 4C2)/(30C5)`

Pr(2 defective) = (2600 *6)/142506

Pr(2 defective) = 0.11

P(at most 2 defective) = 0.46 + 0.42 + 0.11

P(at most 2 defective) = 0.99

3) Probability that at least one bulb is defective = Pr(1 defective) + Pr(2 defective) + Pr(3 defective) + Pr(4 defective)

Pr(1 defective) =0.42

Pr(2 defective) = 0.11

Pr(3 defective) =
`(26C2 * 4C3)/(30C5)`

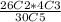
Pr(3 defective) = 0.009

Pr(4 defective) =
`(26C1 * 4C4)/(30C5)`

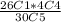
Pr(4 defective) = 0.00018

Pr(at least 1 defective) = 0.42 + 0.11 + 0.009 + 0.00018

Pr(at least 1 defective) = 0.54