Question

Determine the maximum r-value of the polar equation r= 3+3 cos theta

Answer 1

Explanation:

Hi there,

To get started, recall that the cosθ of an angle has a definite maximum value, which is:

`x_m_a_x = cos\theta\leq 1` Hence the cosine of any angle can never be greater than 1, which is illustrated if you plot the graph of cos(x) on a graphing calculator or Desmos.com. Thus, 1 is the maximum of cosθ; the same goes for sinθ, but at a different angle.

With this in mind, plug this in:

`r = 3 + (3)cos\theta=3+(3)(1) = 3+3 =6\\r=6`

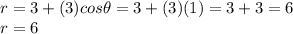
Therefore, the maximum r-value from this polar equation is 6.

If you are adept in calculus, this equation can also be solved using a derivative and some trigonometry:

`(d)/(d\theta) [r]=(dr)/(d\theta) = (d)/(d\theta) (3)+(3)(d)/(d\theta) (cos\theta)\\(dr)/(d\theta) =0+(3)(-sin\theta)\\`

In calculus, the maximum of a function is when its rate is equal to zero:

`\\(dr)/(d\theta)=0=0+(3)(-sin\theta)\\0=-3sin\theta\\0=sin\theta`

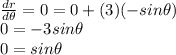
Sine of a RADIANS angle is only equal to zero when θ is equal to the following:

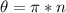`\theta=\pi *n` where n=0,1,2,3,... and π is in radians

Hence plug in 0 into the original equation for θ to make cosine a maximum:

r=3 + 3(cos0) = 3 +3(1) = 6

Same answer obtained!

If you liked this solution, please hit Thanks or give a Rating!