Answer:
878 years
Explanation:
The amount of carbon-14 present in animal bones after t years is given by:

If the bone has lost 10% of its carbon-14.
Its Initial Amount of C-14,
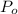 =100%=1
=100%=1
Present Amount, P(t)=(100-10)%=90%=0.9
Substituting these values in the model

The bone is 878 years old.