Answer: 37 units
Explanation:
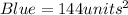 This also works as the height of the triangle.
This also works as the height of the triangle.
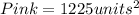 This also works as the base of the triangle.
This also works as the base of the triangle.
Let's call pink ''a'', and blue ''b''. The side we're looking for ''c'' is the hypothenuse.
To find the values of a and b, use the area formula of a square and solve for a side. In this case, since we're going to need the squared values, this step can be omitted.
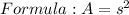
![s=\sqrt[]{A}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/zefbuu3vmd3mt47uik0qk9e9vf4uwrlsmk.png)
Let's work with Blue.
![s=\sqrt[]{144units^2} \\s=12units](https://img.qammunity.org/2021/formulas/mathematics/middle-school/tvq6uaaq1yub9b3abrusds0m0yldruzkqt.png)
Now Pink.
![s=\sqrt[]{1225units^2}\\s=35units](https://img.qammunity.org/2021/formulas/mathematics/middle-school/obwibs0qm8apll7vw9972el1n9fbuj34mz.png)
So we have a triangle with a base of 35 units and a height of 12 units.
Now let's use the pythagoream's theorem to solve.
![c^2=a^2+b^2\\c=\sqrt[]{a^2+b^2} \\c=\sqrt[]{(12units)^2+(35units)^2}\\c=\sqrt[]{144units^2+1225units^2}\\ c=\sqrt[]{1369units^2}\\ c=37units](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ehhu8b0enw9q6vb6sy6wlxopchbcxre7ez.png)