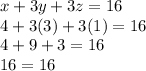Question

Find the complete solution of the linear system, or show that it is inconsistent.

x + y + z = 8
x + 3y + 3z = 16
2x + y − z = 10

Answer 1

`x=4\\y=3\\z=1`

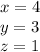
Explanation:

`(a) x+y+z=8\\(b)x+3y+3z=16\\(c)2x+y-z=10`

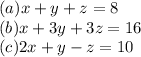
Let's add equation a and c to make a new equation in which z is not a variable.

`x+y+z=8\\2x+y-z=10`

--------------------------

`(d)3x+2y=18`

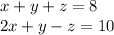
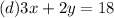
Now let's add equation b and c, but first, multiply equation c by 3, so that the z's will be eliminated.

`(3)(2x+y-z=30)\\(e)6x+3y-3z=30`

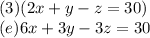
Add b and e.

`x+3y+3z=16\\6x+3y-3z=30`

-----------------------------------

`(f)7x+6y=46`

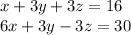
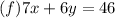
Now you have a two variable system of equations (d and f)

`3x+2y=18\\7x+6y=46`

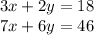
You can solve this by multiplying by equation d by 6 and equation f by -2

`(6)(3x+2y=18)\\(-2)(7x+6y=46)`

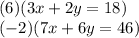
Leaving our equations like;

`18x+12y=108\\-14x-12y=-92`

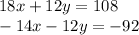
Add them to eliminate y

`18x+12y=108\\-14x-12y=-92`

--------------------------------

`4x=16`

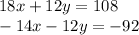
solve for x;

`x=(16)/(4) \\x=4`

Replace x in either d or f, to find y

`3x+2y=18`

`3(4)+2y=18\\12+2y=18\\2y=18-12\\2y=6\\y=(6)/(2)\\ y=3`

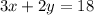
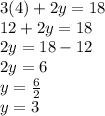
Now that you have found x and y, replace them in either a, b, or c, to find z

`x+y+z=8\\4+3+z=8\\7+z=8\\z=8-7\\z=1`

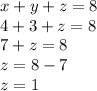
To make sure that you have found the right values, replace all three variables in any of the equations and it should be equal.

`x+3y+3z=16\\4+3(3)+3(1)=16\\4+9+3=16\\16=16`