Answer:
34.77°
Explanation:
In a triangle with sides a, b, and c, the law of cosines tells us that
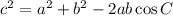 , where C is the angle between sides a and b and across from side c. On this triangle, we can say a = 14, b = 11, c = 8, and C = m∠B; plugging these values in, we have
, where C is the angle between sides a and b and across from side c. On this triangle, we can say a = 14, b = 11, c = 8, and C = m∠B; plugging these values in, we have

Simplifying this equation:

to unwrap this, we can put each side through the inverse cosine function:
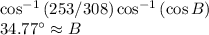
And we have our result for m∠B.