Answer:
12.3 feet.
Explanation:
As we are given that
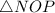 is an right angled triangle.
is an right angled triangle.

And we have to find out the value of side OP to the nearest tenth of a foot by rounding off the value as seen in the attached figure as well.
By using Trigonometric functions in a right angled
 , we know that:
, we know that:
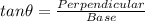
Here,
 is
is
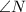 , Perpendicular is side OP and Base is side PN.
, Perpendicular is side OP and Base is side PN.
So,

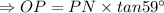
Putting the values of PN and
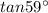 .
.

Hence, the value of OP is
 .
.