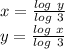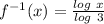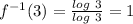Answer:
1
I've attached a screenshot from my graphing calculator of
 in blue and
in blue and
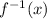 in red. Notice how the red line (inverse function) has (3, 1)
in red. Notice how the red line (inverse function) has (3, 1)
Explanation:
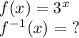
We must first figure out the inverse function of
 which is
which is
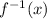

We say y = f(x) to begin with, but after find x = ...
we must 'swap' x and y