Question

5. How long is the diagona of a 12 ft-by-16 ft rectangular garden?

A. 6 ft
B. 14 ft
C. 18 ft
D. 20 ft

Answer 1

D. 20 ft

Explanation:

Use pythagorus! We can imagine the rectangle is split into 2 equal triangles, one side of the triangle being 12, and the width being 16.

Pythagorus theorum is used to calculate the hypotenuse (long side) of a right-angled triangle. This is the formula:

`\sf{a^(2)+b^(2) = c^(2) }`

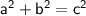
So, we do 12^2 (squared) + 16^2 =

144 + 256 = 400

Now, we have to find the square root of 400, which is equal to

20

So our answer is 20ft

Hope this makes sense! If you need further explanation, do let me know...

- profparis

Answer 2

The correct answer is option D, 20ft

Explanation:

After drawing the picture below, you can just use pythagorean theorem to solve for the diagonal, or the hypotenuse in this case;

(Length)² + (Width)² = (Diagonal)²

(16)² + (12)² = (Diagonal)²

256 + 144 = (Diagonal)²

400 = (Diagonal)²

`√(400)` =
`\sqrt{Diagonal^(2) }`

20 = Diagonal

Hope this helps!