Question

A 400. g sample of strontium 90 is allowed to decay for 280 years.

If Sr-90 has a half life of 28 years, how much Sr-90 remains?
How much total mass remains (Sr-90 and more stable isotopes combined)?
What quantity of more stable isotopes exist?

Answer 1

Question:

a. If Sr-90 has a half life of 28 years, how much Sr-90 remains?

b. How much total mass remains (Sr-90 and more stable isotopes combined)?

c. What quantity of more stable isotopes exist?

Answer:

a. 25/64 grams

b. 400 g

c. 399.61 g

Step-by-step explanation:

The formula for calculating half life is as follows;

`N(t) = N_0 ((1)/(2) )^{(t)/(t_(1/2))`

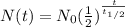
Where:

N(t) = Quantity of the remaining substance

N₀ = Initial radioactive substance quantity = 400

t = Time duration = 280 years

`t_(1/2)` = Half life of the radioactive substance = 28 years

a. Plugging in the values we have;

`N(t) = 400((1)/(2) )^{(280)/(28) }= (25)/(64 ) \ grams`

Therefore, the amount of Sr-90 that remains after 280 years is 25/64 or 0.391 grams

b. The amount of the total mass that remains is constant = 400 g

c. The quantity of the more stable isotopes that exits is therefore, 400 - 0.391 = 399.61 grams