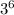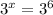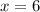Question

How do you evaluate logarithms? Explain using an example or mathematical evidence to support your answer.

Answer 1

Answer: Explanation below.

Explanation:

First of all you need to know how to convert a logarithm into an exponential expression. The property is:

`log_Bx=n`

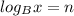
This is the same as:
`B^n=x`

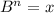
Example 1:

`log_99=`

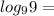
We are trying to find what to raise 9 to, in order to get a result of 9.

`9^x=9`

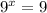
When you have same bases, you equal exponents.

`x=1`

Therefore;
`log_99=1`

Example 2:

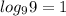
`log_232=`

`2^x=32`

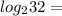
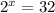
In this case, we have to make sure both sides have the same base. 32 can have a base of 2 if expressed as:
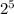`2^5` which is 2*2*2*2*2

Rewriting this example we have;

`2^x=2^5`

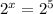
Since we have the same base, we equal exponents.

`x=5`

Therefore;
`log_232=5`

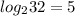
Example 3:

`log_3729=`

`3^x=729`

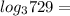
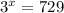
729 can have a base of 3 if expressed as:
`3^6`

`3^x=3^6`

`x=6`

Answer 2

use a calculator

Explanation:

The logarithm function is a transcendental function not generally amenable to calculation by hand (possibly except when logarithms are small integers). It can only be evaluated for numbers. The logs of variable expressions can only be indicated.

Attached is an example of a calculator giving the natural log of 2.

_____

Comment on hand calculation

Before the advent of computers, logarithms were calculated by hand. It often took many years of calculation to produce usable tables of logarithms. Not only were logs of numbers provided in tables, but also logs of trig functions of angles. The latter greatly aided global navigation, making it possible to easily compute navigation functions.