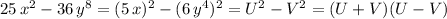Answer:

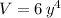
Explanation:
Recall that an expression that can be factored as (U+V)(U-V) using distributive property for multiplication of binomials, should render:
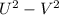 (the factorization given above is that of a difference of squares. Then, the idea is to write the original expression :
(the factorization given above is that of a difference of squares. Then, the idea is to write the original expression :

as a difference of perfect squares. Let's examine each term and its numerical and variable form to find if they can be written as perfect squares:
a) the term
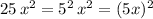 therefore, if we assign the letter U to
therefore, if we assign the letter U to
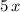 , the first term becomes:
, the first term becomes:
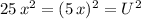
b) the term
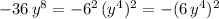 therefore, if we assign the letter V to
therefore, if we assign the letter V to
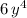 , this second term becomes:
, this second term becomes:
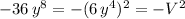
With the above identification, our expression can now be factored as a difference of squares: