Answer:
470 °C
Step-by-step explanation:
This looks like a case where we can use Charles’ Law:

Data:
V₁ = 20 L; T₁ = 100 °C
V₂ = 40 L; T₂ = ?
Calculations:
(a) Convert the temperature to kelvins
T₁ = (100 + 273.15) K = 373.15 K
(b) Calculate the new temperature
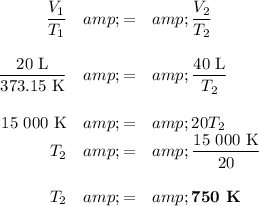
Note: The answer can have only two significant figures because that is all you gave for the volumes.
(c) Convert the temperature to Celsius
T₂ = (750 – 273.15) °C = 470 °C