Question

`\displaystyle\rm\int \limits_(0)^{ (\pi)/(2) } \sqrt[3]{tanx} \ln(tanx)dx`​

Answer 1

Replace
`x\mapsto \tan^(-1)(x)` :

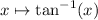`\displaystyle \int_0^(\frac\pi2) \sqrt[3]{\tan(x)} \ln(\tan(x)) \, dx = \int_0^\infty \frac{\sqrt[3]{x} \ln(x)}{1+x^2} \, dx`

Split the integral at x = 1, and consider the latter one over [1, ∞) in which we replace
`x\mapsto\frac1x` :

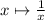`\displaystyle \int_1^\infty \frac{\sqrt[3]{x} \ln(x)}{1+x^2} \, dx = \int_0^1 \frac{\ln\left(\frac1x\right)}{\sqrt[3]{x} \left(1+\frac1{x^2}\right)} (dx)/(x^2) = - \int_0^1 \frac{\ln(x)}{\sqrt[3]{x} (1+x^2)} \, dx`

Then the original integral is equivalent to

`\displaystyle \int_0^1 (\ln(x))/(1+x^2) \left(\sqrt[3]{x} - \frac1{\sqrt[3]{x}}\right) \, dx`

Recall that for |x| < 1,

`\displaystyle \sum_(n=0)^\infty x^n = \frac1{1-x}`

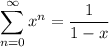
so that we can expand the integrand, then interchange the sum and integral to get

`\displaystyle \sum_(n=0)^\infty (-1)^n \int_0^1 \left(x^(2n+\frac13) - x^(2n-\frac13)\right) \ln(x) \, dx`

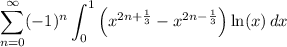
Integrate by parts, with

`u = \ln(x) \implies du = \frac{dx}x`

`du = \left(x^(2n+\frac13) - x^(2n-\frac13)\right) \, dx \implies u = (x^(2n+\frac43))/(2n+\frac43) - (x^(2n+\frac23))/(2n+\frac23)`

`\implies \displaystyle \sum_(n=0)^\infty (-1)^(n+1) \int_0^1 \left((x^(2n+\frac43))/(2n+\frac43) - (x^(2n+\frac13))/(2n-\frac13)\right) \, dx \\\\ = \sum_(n=0)^\infty (-1)^(n+1) \left(\frac1{\left(2n+\frac43\right)^2} - \frac1{\left(2n+\frac23\right)^2}\right) \\\\ = \frac94 \sum_(n=0)^\infty (-1)^(n+1) \left(\frac1{(3n+2)^2} - \frac1{(3n+1)^2}\right)`

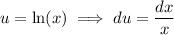
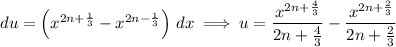
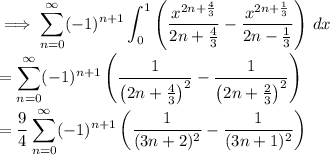
Recall the Fourier series we used in an earlier question [27217075]; if
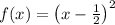`f(x)=\left(x-\frac12\right)^2` where 0 ≤ x ≤ 1 is a periodic function, then

`\displaystyle f(x) = \frac1{12} + \frac1{\pi^2} \sum_(n=1)^\infty (\cos(2\pi n x))/(n^2)`

`\implies \displaystyle f(x) = \frac1{12} + \frac1{\pi^2} \left(\sum_(n=0)^\infty (\cos(2\pi(3n+1)x))/((3n+1)^2) + \sum_(n=0)^\infty (\cos(2\pi(3n+2)x))/((3n+2)^2) + \sum_(n=1)^\infty (\cos(2\pi(3n)x))/((3n)^2)\right)`

`\implies \displaystyle f(x) = \frac1{12} + \frac1{\pi^2} \left(\sum_(n=0)^\infty (\cos(6\pi n x + 2\pi x))/((3n+1)^2) + \sum_(n=0)^\infty (\cos(6\pi n x + 4\pi x))/((3n+2)^2) + \sum_(n=1)^\infty (\cos(6\pi n x))/((3n)^2)\right)`

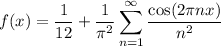
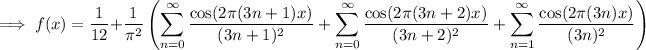
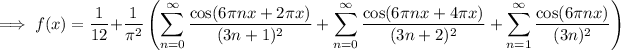
Evaluate f and its Fourier expansion at x = 1/2 :

`\displaystyle 0 = \frac1{12} + \frac1{\pi^2} \left(\sum_(n=0)^\infty ((-1)^(n+1))/((3n+1)^2) + \sum_(n=0)^\infty ((-1)^n)/((3n+2)^2) + \sum_(n=1)^\infty ((-1)^n)/((3n)^2)\right)`

`\implies \displaystyle -(\pi^2)/(12) - \frac19 \underbrace{\sum_(n=1)^\infty ((-1)^n)/(n^2)}_{-(\pi^2)/(12)} = - \sum_(n=0)^\infty (-1)^(n+1) \left(\frac1{(3n+2)^2} - \frac1{(3n+1)^2}\right)`

`\implies \displaystyle \sum_(n=0)^\infty (-1)^(n+1) \left(\frac1{(3n+2)^2} - \frac1{(3n+1)^2}\right) = (2\pi^2)/(27)`

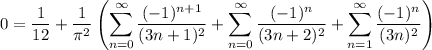
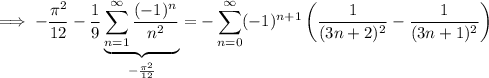
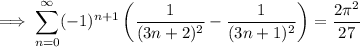
So, we conclude that

`\displaystyle \int_0^(\frac\pi2) \sqrt[3]{\tan(x)} \ln(\tan(x)) \, dx = \frac94 * (2\pi^2)/(27) = \boxed{\frac{\pi^2}6}`