Question

During a rock concert, the noise level (in decibels) in front row seats has a mean of 92 dB with a standard deviation of 9 dg_ Without

assuming a normal distribution, find the minimum percentage of noise level readings within 8 standard deviations of the mean. (Round
your answer to 2 decimal places.)
Minimum percentage

Answer 1

The minimum percentage of noise level readings within 8 standard deviations of the mean is 98.44%.

Explanation:

When we do not know the shape of the distribution, we use the Chebyshev's Theorem to find the minimum percentage of a measure within k standard deviations of the mean.

This percentage is:

`p = 1 - (1)/(k^(2))`

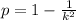
Within 8 standard deviations of the mean

This means that
`k = 8`. So

`p = 1 - (1)/(8^(2)) = 1 - (1)/(64) = (64 - 1)/(64) = (63)/(64) = 0.9844`

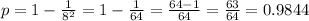
The minimum percentage of noise level readings within 8 standard deviations of the mean is 98.44%.