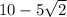Question

Given:

Triangle MDL
Circle O is inscribed in triangle
m∠M=m∠L=45°
MD = 10
Find: the radius of the circle

Answer 1

10-5
`√(2)`

Explanation:

As per the attached figure, right angled
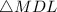`\triangle MDL` has an inscribed circle whose center is
`I`.

We have joined the incenter
`I` to the vertices of the
`\triangle MDL`.

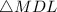Sides MD and DL are equal because we are given that
`\angle M = \angle L = 45 ^\circ.`

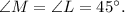
Formula for area of a
`\triangle = (1)/(2) * base * height`

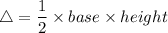
As per the figure attached, we are given that side a = 10.

Using pythagoras theorem, we can easily calculate that side ML = 10
`√(2)`

Points P,Q and R are at
`90 ^\circ` on the sides ML, MD and DL respectively so IQ, IR and IP are heights of
`\triangle`MIL,
`\triangle`MID and
`\triangle`DIL.

Also,

`\text {Area of } \triangle MDL = \text {Area of } \triangle MIL +\text {Area of } \triangle MID+ \text {Area of } \triangle DIL`

`(1)/(2) * 10 * 10 = (1)/(2) * r * 10 + (1)/(2) * r * 10 + (1)/(2) * r * 10\sqrt2\\\Rightarrow r = \frac {10}{2+\sqrt2} \\\Rightarrow r = (5\sqrt2)/(\sqrt2+1)\\\text{Multiplying and divinding by }(\sqrt2 +1)\\\Rightarrow r = 10-5\sqrt2`

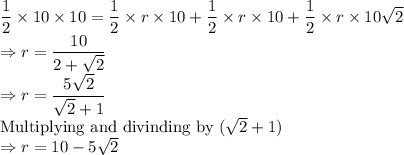
So, radius of circle =
`10-5\sqrt2`