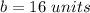Answer:
The length of each side of tyhe nonagon is 16 units
Explanation:
step 1
Find the perimeter of nonagon
we know that
The area of any regular polygon is given by the formula
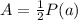
where
P is the perimeter
a is the apothem
we have
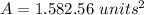
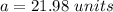
substitute
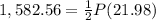
solve for P
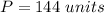
step 2
Find the length side of nonagon
we know that
The perimeter of nonagon is given by the formula
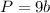
where
b is the length side of nonagon
we have
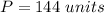
substitute
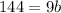
solve for b