Answer:
The graph is a horizontal hyperbola with vertices at (-5,0) and (5,0).
Explanation:
The given formula is
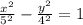
Notice that the negative variable is
 , that means the hyperbola is horizontal. Also, its focal poitns are on the x-axis and have the form
, that means the hyperbola is horizontal. Also, its focal poitns are on the x-axis and have the form
 and
and
 .
.
Remember that the parameter
 is always with the positive varible. So,
is always with the positive varible. So,
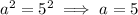
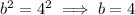
The asymptotes are
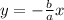 and
and
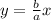 , replacing parameters, we have
, replacing parameters, we have
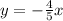 and
and
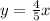
So, the hyperbola is shown in the image attached, there you can observe that the vertices are
 and
and
 , which matches the parameter
, which matches the parameter
 .
.