Answer:
A) x-intercepts are (0.6, 0) and (-1, 0)
B) vertex is (-0.2, -3.2)
C) see attached
Explanation:
Part A
Given function:
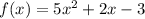
The x-intercepts are when f(x) = 0
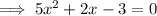
To factor, find two numbers that multiply to -15 and sum to 2: 5 and -3
Rewrite the middle term of the quadratic as the sum of these number:
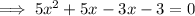
Factorize the first two terms and the last two terms separately:
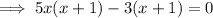
Factor out the common term
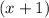 :
:
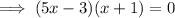
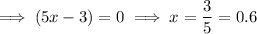
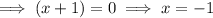
Therefore, the x-intercepts are (0.6, 0) and (-1, 0)
Part B
As the leading coefficient of the quadratic is positive, the parabola will open upwards. This means that the vertex will be a minimum point.
The x-coordinate of the vertex is the midpoint of the zeros.
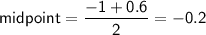
To find the y-coordinate of the vertex, substitute the found value of x into the given equation:
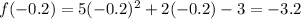
Therefore, the vertex is (-0.2, -3.2)
Part C
Plot the zeros and the vertex.
The axis of symmetry is the x value of the vertex, so ensure that the graph is symmetrical about x = -0.2.