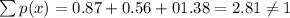Question

Which of the following represents a valid probability distribution? A 2-column table labeled Probability Distribution A has 4 rows. The first column is labeled x with entries 1, 2, 3, 4. The second column is labeled P (x) with entries negative 0.14, 0.6, 0.25, 0.29. A 2-column table labeled Probability Distribution B has 4 rows. The first column is labeled x with entries 1, 2, 3, 4. The second column is labeled P (x) with entries 0, 0.45, 0.16, 0.39. A 2-column table labeled Probability Distribution C has 4 rows. The first column is labeled x with entries 1, 2, 3, 4. The second column is labeled P (x) with entries 0.45, 1.23, negative 0.87, 0.19. A 2-column table labeled Probability Distribution D has 4 rows. The first column is labeled x with entries 1, 2, 3, 4. The second column is labeled P (x) with entries 0.87, 0.56, 0, 1.38.

Answer 1

B

Explanation:

source: trust me bro

jk, Edge 2022. took test

Answer 2

B

Explanation:

The key to solving this is knowing that the sum of probability distribution is always 1.

That is:
`\sum p(x)=1`

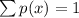
Out of all the tables, only the table below satisfies this condition.

A 2-column table labeled Probability Distribution B has 4 rows. The first column is labeled x with entries 1, 2, 3, 4. The second column is labeled P (x) with entries 0, 0.45, 0.16, 0.39.

`\sum p(x)=0+0.45+0.16+0.39=1`

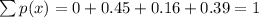
Check

Option A:
`\sum p(x)=0.14+0.6+0.25+0.29=1.28\\eq 1`

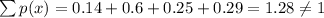
Option C:
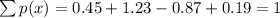`\sum p(x)=0.45+1.23-0.87+0.19=1`, but probability cannot be negative

Option D:
`\sum p(x)=0.87+0.56+01.38=2.81\\eq 1`