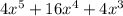Answer:
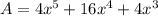
Explanation:
The area of a trapezoid is found with the formula
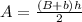
where B is the measurement of the longest side of the trapezoid (the largest base) and b is the measurement of the shortest side of the trapezium (the minor base), and h is the height. In this case we have:

so, substituting this values in the formula:
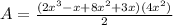
Simplifying the expression and joining like terms
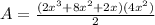
Multiplying the numerator parentheses:
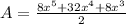
dividing by 2:
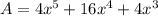
the simplified expression for the area of this trapezoid is