Answer:
9/20
Step-by-step explanation:
Total number of candies =60
Number of Green candies, n(G)=36
Number of candies with caramel, n(C)=45
Since the events are independent, the probability of selecting two candies where the first is green and the second has caramel is given by:
P(GC)=P(G) X P(C)
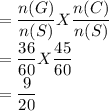
The probability in its lowest form is 9/20.