Question

Say you buy an house as an investment for 250000$ (assume that you did not need a mortgage). You estimate that the house will increase in value continuously by 31250$ per year. At any time in the future you can sell the house and invest the money in a fund with a yearly interest rate of 8.5% compounded bi-monthly.

If you want to maximize your return, after how many years should you sell the house? Report your answer to 1 decimal place.

Answer 1

3.3 years

Explanation:

Let the price of the house when it is being sold be = x

The Annual return received from the fund after a year that house is being sold is : A - P

where ;

P = current market price

A = price after one year

A is given by the formula:

`A = P (1+ (r)/(n) )^{{n}{t} }`

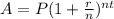
where ; P = x

r = 8.5% = 0.085

n = 12

t = 1

`A= x(1+(0.085)/(2))^(12*1)`

`A= x(1.00708333)^(12)`

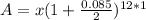
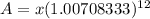
A = 1.08839 x

The annual return is A - P = 1.08839 x - x

= 0.08839x

However, the house should be sold when this return is equivalent to the annual increase in value of the house

∴ 0.08839x = 31250

`x = (31250)/(0.08839) \\ \\ x = 353546.78`

Thus , the current price (x) = $353546.78

Profit till that time = Current price - Initial Price

= (353546.78- 250000)$

= $103546.78

The time taken for this much profit to accumulate =
`(Total \ profit)/(Annual \ profit)`

=
`(103546.78)/(31250)`

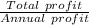
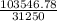
= 3.3135

≅ 3.3 years ( to one decimal place)