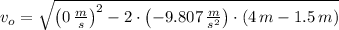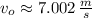Answer:
a) Yes, b)
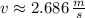 , c)
, c)
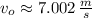
Explanation:
a) The maximum height reached by the rock is:
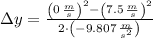
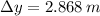
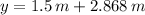
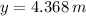
Yes, the rock will exceed the top of the wall.
b) The speed when the rock reaches the top of the wall:
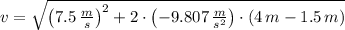
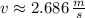
c) The initial speed required so that stone does not exceed the top of the wall is: