Question

Whats the surface area of a cone with a height of "50" and a diameter of "40"

Answer 1

4637.883499 units²

Explanation:

Radius 'r'

40/2 = 20

Slant height 's'

sqrt(20²+50²) = 10sqrt(29)

Surface area:

(pi × r × s) + (pi × r²)

[3.14×20×10sqrt(29)] + (3.14×20²)

4637.883499 units²

Answer 2

56844.9 units squared

Explanation:

The surface area of a cone is denoted by:
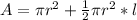`A=\pi r^2+(1)/(2) \pi r^2*l` , where r is the radius and l is the slant height. The slant height is basically the length from a point on the base circle to the top vertex of the cone.

Here, since our diameter is 50 and diameter is twice the radius, then our radius is r = 50/2 = 25.

To find the slant height, we have to use the Pythagorean Theorem:

`l^2=r^2+h^2`, where h is the height

`l^2=25^2+50^2=625+2500=3125`

`√(l^2) =√(3125)`

`l=25√(5)`

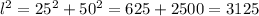
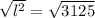
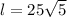
Now, plug these values of r and l into the first equation above:

`A=\pi r^2+(1)/(2) \pi r^2*l`

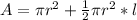
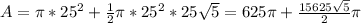`A=\pi *25^2+(1)/(2) \pi *25^2*25√(5) =625\pi +(15625√(5) )/(2) \pi` ≈ 56844.9 units squared