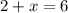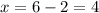Question

Find the value of x in the equation without evaluating the power

Answer 1

4

Explanation:

Here's my method of doing this:

We'll be using logarithms

Our question is:

`((1)/(3))^(2)` ×
`((1)/(3))^x` =
`(1)/(729)`

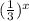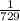
If we don't want to evaluate any powers at all we'll have to make each term have the same base (so that we can ignore the base —
`(1)/(3)`)

we need to figure out what power of a
`(1)/(3)` the
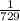`(1)/(729)` is.

what we can do is the following:

`((1)/(3))^?` =
`(1)/(729)`

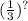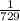
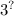`3^?` = 729

If we take the "log" of each, we can find out what power of 3 gives 729.
`log(3^?) = log\ 729`

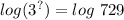
We must remember this rule:
`log(a^n) = n * log(a)`

`? * log 3 = log 729`

`? = (log\ 729)/(log\ 3)`

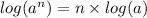
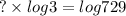
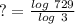
? = 6 (with a calculator)

This means that to get 729, we need to do
`3^6`

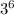
Therefore
`((1)/(3))^6 = (1)/(729)`

We can now solve the equation!

`((1)/(3))^(2)` ×
`((1)/(3))^x` =
`(1)/(729)`

`((1)/(3))^(2)` ×
`((1)/(3))^x` =
`((1)/(3))^6`

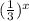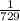
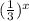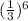
Since each term of our equation has the same base of
`(1)/(3)` we can ignore it and just deal with the powers!

We must remember this rule:
`x^a * x^b = x^(a + b)`

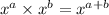
Using this rule:

`((1)/(3))^(2)` ×
`((1)/(3))^x` =
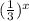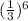`((1)/(3))^6` becomes...

`2 + x = 6`

`x = 6 - 2 = 4`