Question

Find the Area of the figure below, composed of an isoceles trapezoid and one

semicircle. Rounded to the nearest tenths place

Answer 1

the total area is 15.6 square units

Explanation:

hello,

you can find the total area dividing the shape into two known shapes

total area= area of the trapezoid +area of the semicircle

then

step one

find the area of the isosceles trapezoid using

`A=(a+b)/(2)*h`

where

a is the smaller base

b is the bigger base

h is theheight

A is the area

let

a=2

b=5

h=4

put the values into the equation

`A=(a+b)/(2)*h\\A=(5+2)/(2)*4\\A=3.5*4\\A=14`

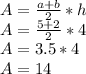
Step two

find the area of the semicircle

the area of a circle is given by

`A_(c)=\pi (d^(2))/(4)\\`

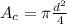
but, we need the area of half circle, we need divide this by 2

`A_(semic)=( \pi (d^(2))/(4))/(2)\\A_(semic)= \pi (d^(2))/(8)`

now the diameter of the semicircle is 2, put this value into the equation

`A_(semic)= \pi (2^(2))/(8)\\\\A_(semic)= \pi (1)/(2)\\ A_(semic)=(\pi )/(2)\\`

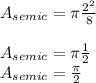
find the total area

total area= area of the trapezoid +area of the semicircle

`total\ area= 14+(\pi )/(2) \\total\ area=15.6`

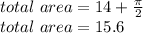
so, the total area is 15.6 square units

Have a good day.