Answer:
Pythagorean Theorem!
Explanation:
First, we have to find the lengths of each side.
To do that, we need to assign variables:
x-Length of side AB
y-Length of side BC
z-Length of side AC
(This is because if you don't assign variables, you automatically get the question wrong in Middle School)
So to find the lengths, we need "Pythagorean Theorem"(In reality it's called the distance formula, but it works on the same principle:
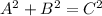 , where C is the hypotenuse, check the attached file, and A and B are the legs, and imagine that C is our side of the triangle)
, where C is the hypotenuse, check the attached file, and A and B are the legs, and imagine that C is our side of the triangle)
So, the Distance Formula is this:
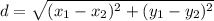
Where, D is our triangle side length, and x_1, x_2 are the X's of our coordinates(same goes for y):
So, let's solve!
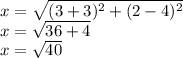
So, we found x! (Don't Confuse this variable x with our other X's, the coordinate values)
Solving for the other ones!
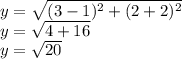
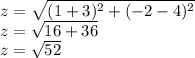
So, then, we just have to add them!
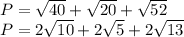
It cannot be simplified any further, so we have to use a calculator!
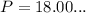
So, there is your Answer! The Perimeter is about 18 Units!
Hope this helps!
Stay Safe!
P.S. Pheww... Took me a long time to write that!