Question

A standard number cube has 6 sides labeled 1 to 6. apu rolls a standard number cube 30 times. How many times can

he expect to roll a 5 or 6?

Answer 1

Or you could do it more simply , the answer is 10

Explanation:

First of all 5 and 6 are 2 out of 6 numbers so 2/6 and simplified that is 1/3. Then you multiply 1/3 x30/1 which equals 30/3 which is an improper fraction so the answer is 30 divided by 3 and that is 10.

The answer is 10 :)

Answer 2

The expected value of rolling a 5 or 6 is 10.

Explanation:

The sample space of rolling a standard number cube is:

S = {1, 2, 3, 4, 5 and 6}

The cube is standard, this implies that each side has an equal probability of landing face-up.

So, the probability of all the six outcomes is same, i.e.
`(1)/(6)`.

Now it is provided that Apu rolls the cube n = 30 times.

Let the random variable X represent the value on the face of cube.

The event of rolling a 5 and rolling a 6 are mutually exclusive, i.e. they cannot occur together.

So, P (X = 5 and X = 6) = 0.

Compute the probability of getting a 5 or 6 as follows:

P (X = 5 or X = 6) = P (X = 5) + P (X = 6) - P (X = 5 and X = 6)

= P (X = 5) + P (X = 6)

`=(1)/(6)+(1)/(6)\\\\=(2)/(6)\\\\=(1)/(3)`

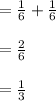
Compute the expected value of rolling a 5 or 6 as follows:

`E(X = 5\ \text{or}\ X = 6)=n* P(X = 5\ \text{or}\ X = 6)`

`=30* (1)/(3)\\\\=10`

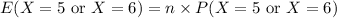
Thus, the expected value of rolling a 5 or 6 is 10.