Question

suppose your friends parents invest $15000 in an account paying 6% compounded annually. what will the balance be after 8 years

Answer 1

$23,907.72

Explanation:

Lets use the compound interest formula to solve:

`A=P(1+(r)/(n) )^(nt)`

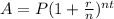
P = initial balance

r = interest rate (decimal)

n = number of times compounded annually

t = time

First, lets change 6% into a decimal:

6% ->
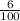`(6)/(100)` -> 0.06

Next, plug the values into the equation:

`A=15,000(1+(0.06)/(1))^(1(8))`

`A=23,907.72`

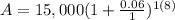
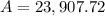
The balance after 8 years will be $23,907.72