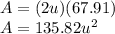Question

The area of the circular base of a cylinder is 367 square units. The height of the cylinder is 2 units.

What is the lateral area of the cylinder? Express the answer in terms of A.
127 square units
240 square units
O 604 square units
72 square units

Answer 1

`A=135.82u^2`

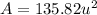
Explanation:

The formula to calculate the lateral area of a cylinder is:

`A=h*c`

where h is the height of the cylinder, and c is the circumference (perimeter) of the circular base:

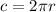`c=2\pi r` where r is the radius

To calculate the circumference we need the radius of the circle, which we can calculate because we know that the area the circle is:

`367u^2`,

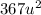substituting this in the formula for the area of a circle:

`A_(c)=\pi r^2`

`367u^2=\pi r^2`

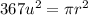
and solving for the radius:

`(367u^2)/(\pi)=r^2\\\\\sqrt{(367u^2)/(\pi ) }=r\\\\\sqrt{(367u^2)/(3.1416) }=r\\\\10.808u=r`

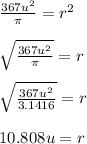
now that we know the radius, we calculate the circumference:

`c=2\pi r\\c=2\pi (10.808u)\\c=67.91u`

and finally we go back to the formula for the lateral area:

`A=h*c`

and substitute the height:
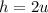`h=2u` and the circumference:

`A=(2u)(67.91)\\A=135.82u^2`