Question

I need someone to help me do this, see attached documents for the questions

Answer 1

1.) 20.2

Explanation:

1.) You need to use the distance formula:

`d=\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

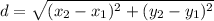
Find the distance of A to B first:

`(-2,2)(3,2)\\\\√((3+2)^2+(2-2)^2)\\\\√((5)^2+(0)^2)\\\\√(25) =5`

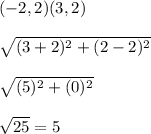
B to C:

`(3,2)(-1,-5)\\\\√((-1-3)^2+(-5-2)^2)\\\\√((-4)^2+(-7)^2)\\\\√(16+49)\\\\√(65) =8.06=8.1`

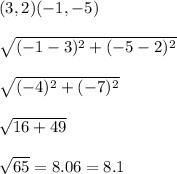
C to A:

`(-1,-5)(-2,2)\\\\√((-2+1)^2+(2+5)^2)\\\\√((-1)^2+(7)^2)\\\\√(1+49)\\\\√(50)=7.07=7.1`

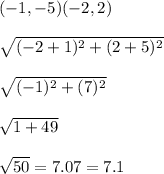
Add distances to find the perimeter:

`5+8.1+7.1=20.2`

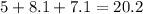
2.) Part A:

You need to use the mid-point formula:

`midpoint=((x_(1)+x_(2))/(2) ,(y_(1)+y_(2))/(2) )`

`(3,2)(7,11)\\\\((3+7)/(2),(2+11)/(2))\\\\((10)/(2),(13)/(2))\\\\m=( 5,6.5)`

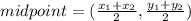
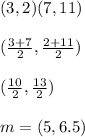
Part B:

1. Use the slope-intercept formula:

`y=mx+b`

M as the slope, b the y-intercept.

Find the slope of the two points A and B using the slope formula:

`m=(y_(2)-y_(1))/(x_(2)-x_(1)) =(rise)/(run)`

Insert slope as m into equation.

Take point A as coordinates
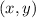`(x,y)` and insert into the equation. Solve for the intercept, b:

`(y)=m(x)+b`

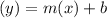
Insert the value of b into the equation.

2. Use the mid-point coordinate. Take the slope.

If you need to find the perpendicular bisector, you will take the negative reciprocal of the slope. Switch the sign and flip it. Ex:

`(1)/(2) =-(2)/(1)=-2\\`

Insert the new slope into the slope-intercept equation as m.

Take the mid-point coordinate as (x,y) and insert into the equation with the new points. Solve for b.

Insert the value of b.