Question

A survey of n = 100 students found that 28 of them were majoring in a STEM field. Give a 95% confidence interval estimate for the true proportion, p, of students who major in a STEM field.

Answer 1

`0.28 - 1.96\sqrt{(0.28(1-0.28))/(100)}=0.192`

`0.28 + 1.96\sqrt{(0.28(1-0.28))/(100)}=0.368`

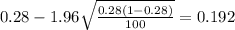
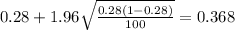
We are 95% that the true proportion of interest for the students were majoring in a STEM field is between 0.192 and 0.368

Explanation:

We want to calculate a confidence interval for the true proportion p who represent the % of students were majoring in a STEM field. The best point of estimate for this proportion is given by:

`\hat p = (X)/(n)= (28)/(100)=0.28`

The confidence interval for the true proportion of interest is given by:

`\hat p \pm z_(\alpha/2)\sqrt{(\hat p (1-\hat p))/(n)}`

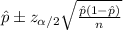
Since the confidence level is 95%, the significance level would be
`\alpha=1-0.95=0.05` and
`\alpha/2 =0.025`. The critical values for this case are:

`z_(\alpha/2)=-1.96, z_(1-\alpha/2)=1.96`

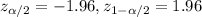
And after replace into the formula we got:

`0.28 - 1.96\sqrt{(0.28(1-0.28))/(100)}=0.192`

`0.28 + 1.96\sqrt{(0.28(1-0.28))/(100)}=0.368`

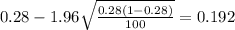
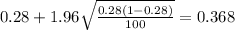
We are 95% that the true proportion of interest for the students were majoring in a STEM field is between 0.192 and 0.368