Question

How many real solutions does x2+6x+13=0 have?

Answer 1

There are NO real solutions to this equation as per the study of its discriminant.

Explanation:

In order to answer the question, one needs to examine the "discriminant" associated with this quadratic equation.

Recall that the discriminant of a quadratic equation of the form:

`a\,x^2+b\,x+c=0`

is given by:
`b^2-4\, (a)\,(c)`

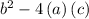
in our case :
`a=1\, ,\,b=6\,, and\,\,\,c=13`

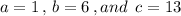
Then the discriminant becomes:

`b^2-4\, (a)\,(c)=6^2-4\,(1)\,(13) =36-52=-16`

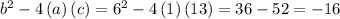
The discriminant is then a negative number, which means that there are NO real solutions (its solutions must involve imaginary numbers)