Answer:

Explanation:
The volume of a pyramid is:
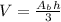
where
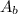 is the area of the base and
is the area of the base and
 is the height (the perpendicular measurement between base and highest point, not the slant height)
is the height (the perpendicular measurement between base and highest point, not the slant height)
Since the base is a square, the area is given by:
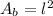
where
 is the length of the side:
is the length of the side:
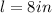 , thus:
, thus:
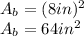
Now we need to find the height, for this we use the right triangle that forms with half of a square side (8in/2 = 4in), the slant height (10in), and the height.
In this right triangle, the slant height is the hypotenuse, the leg 1 is the unknown height, and leg 2 is half of the square side.
Using pythagoras:

substituting our values, and indicating that leg 1 is height h:
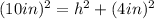
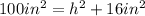
and solving for the height:
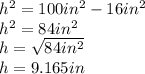
and finally we calculate the volume using this height and the area of the base:
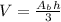
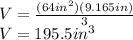
rounding to the nearest cubic inch:
