Answer:
Approximately
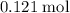 .
.
Step-by-step explanation:
Balance the equation
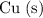 reacts with
reacts with
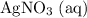 to produce
to produce
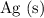 and
and
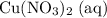 .
.
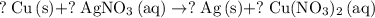 .
.
To balance this equation, start by setting the coefficient of the most complex species to
 . For example,
. For example,
 has more atoms in each of its formula unit than any other species in this reaction. Let the coefficient of
has more atoms in each of its formula unit than any other species in this reaction. Let the coefficient of
 .
.
That formula unit of
 would include:
would include:
The other product,
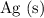 , contains neither
, contains neither
 atoms nor
atoms nor
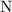 atoms. Therefore, the product side would include exactly
atoms. Therefore, the product side would include exactly
- one
 atom,
atom, - two
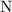 atoms, and
atoms, and - six
 atoms.
atoms.
Atoms are conserved in a chemical reaction. The reactant side shall also include:
Among the reactants,
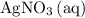 is the only source of
is the only source of
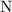 atoms. Each formula unit of
atoms. Each formula unit of
Similarly, the coefficient of
 would be
would be
 .
.
 .
.
There would be exactly

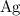 atom on the reactant side (from
atom on the reactant side (from
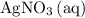 .) The products should also include
.) The products should also include
Hence the equation:
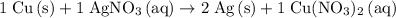 .
.
Calculate n(Cu(NO₃)₂ (aq))
The ratio between the coefficients of
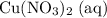 and
and
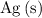 is:
is:
 .
.
Rearrange this equation to obtain:
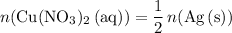 .
.
In other words,
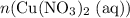 (the number of moles of
(the number of moles of
 that is produced) can be found from
that is produced) can be found from
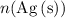 (the number of moles of
(the number of moles of
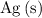 that is produced.)
that is produced.)
On the other hand,
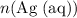 can be found from
can be found from
 (the mass of
(the mass of
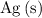 that is produced) using
that is produced) using
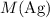 (the formula mass of
(the formula mass of
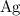 .)
.)
Look up relative atomic mass data of
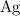 on a modern periodic table:
on a modern periodic table:
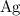 :
:
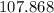 .
.
Therefore, the relative atomic mass of
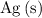 would be:
would be:
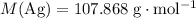 .
.
Calculate
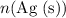 :
:
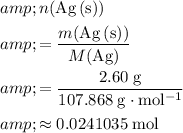 .
.
Calculate
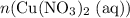 :
:
 .
.