Answer:
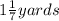
Explanation:
The maximum volume the shipping container can have is 10 cubic yards.
The volume of a rectangular prism is given as:
V = L * W * H
where L is length, W is width and H is height.
To find the maximum height of the container, make H the subject of formula:
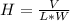
We have been given the length and width of the container as 2 1/2 yards and 3 1/2 yards respectively.
Hence, the maximum height is:
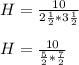

The maximum height of the container is
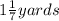 .
.